用字符数组实现2的n次方（大数问题）

为什么要用字符数组实现

在c/c++中，各个类型的数据的精度是有限的，我们可以写一个程序看看各种数据类型可以记录多大范围的数：

#include<stdio.h> 
#include<float.h>
#include<limits.h>
int main()
{
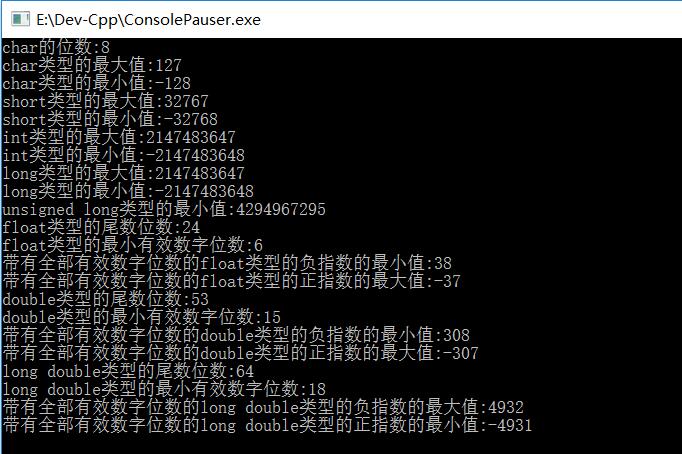
    printf("char的位数:%u\n",CHAR_BIT);
    printf("char类型的最大值:%d\n",CHAR_MAX);
    printf("char类型的最小值:%d\n",CHAR_MIN);
	
	printf("short类型的最大值:%hd\n",SHRT_MAX);
	printf("short类型的最小值:%hd\n",SHRT_MIN);

	printf("int类型的最大值:%d\n",INT_MAX);
	printf("int类型的最小值:%d\n",INT_MIN);

	printf("long类型的最大值:%ld\n",LONG_MAX);
	printf("long类型的最小值:%ld\n",LONG_MIN);
	printf("unsigned long类型的最小值:%lu\n",ULONG_MAX);

	printf("float类型的尾数位数:%u\n",FLT_MANT_DIG);
	printf("float类型的最小有效数字位数:%u\n",FLT_DIG);
	printf("带有全部有效数字位数的float类型的负指数的最小值:%d\n",FLT_MAX_10_EXP);
	printf("带有全部有效数字位数的float类型的正指数的最大值:%d\n",FLT_MIN_10_EXP);

	printf("double类型的尾数位数:%u\n",DBL_MANT_DIG);
	printf("double类型的最小有效数字位数:%u\n",DBL_DIG);
	printf("带有全部有效数字位数的double类型的负指数的最小值:%u\n",DBL_MAX_10_EXP);
	printf("带有全部有效数字位数的double类型的正指数的最大值:%d\n",DBL_MIN_10_EXP);

	printf("long double类型的尾数位数:%d\n",LDBL_MANT_DIG);
	printf("long double类型的最小有效数字位数:%d\n",LDBL_DIG);
	printf("带有全部有效数字位数的long double类型的负指数的最大值:%d\n",LDBL_MAX_10_EXP);
	printf("带有全部有效数字位数的long double类型的正指数的最小值:%d\n",LDBL_MIN_10_EXP);
}

运行以上代码就可以得到各种类型数据的范围，我们可以看出，如果要对整数进行运算，那么2的100次方就已经远远超出long long int所能存储的范围了，这时侯仍然使用long long int就会出错。

如何实现

---

这个时候，一个int存不下，但我们可以用很多个int串起来存，这个时候自然而然的想到了使用字符串，那么如何用字符串实现呢？

#include<iostream>
using namespace std;
int main(){
    const int x=2;//计算x的n次方
	int a[1000] = {0};//开一个长度为1000的数组
	int b = 0;//用来计算向前进的数字，并且第一个数得到的进位是零
	a[999] = 1;
	int n;
	cin >> n;
	for (int i=0;i<n;i++)
	{
		int j=999;
		while(j>=0){
		int k=a[j]*x+b;//这一位乘2之后加上进位
		a[j]=k%10;//除以10取余，实际上是获取本位的数
		b=k/10;//进位的数
		j--;
	}
	}//乘n遍的2
	int s;
	for (s=0;s<1000;s++)
	{
		if(a[s]!=0)
			break;//先循环到不是零的地方
	}
	for (;s<1000;s++){
	cout<<a[s];
	}//从这里开始输出这个数组
	return 0;
}

具体实现方法注释中已经写的很明白了，其实就是循环n次乘法，不过每次乘法的每一位运算，都由自己写出的加法程序运算，这样就能在数组中保存这个大数。
const是用来保存一些全局常量的，这些常量在编译期可以改，在运行期不能改，听起来像宏，其实是用来取代宏的，所以在这里更改x的值，再重新编译，就可以计算其他数的n次冥。
这就是acm中常见的大数问题的一种解决方法，高精度加减乘除在CSDN上也有很多教程，感兴趣的朋友可以去看一看。