我们经常在新闻里听说：距离地球XX光年发生超新星爆炸，距离地球XX光年发现类地行星。且不管新闻真假，真空中电磁波速度是c，要真的用雷达测量几十光年几百光年的距离是不可能实现的，那我们看到这些报道的时候有没有曾怀疑过这些距离是怎么测算的呢？

0x01 天文学距离单位介绍

谈到距离，肯定离不开距离单位，我们平时用到的距离单位放在天体的层面运算的话实在是令人头疼的事情，所以我们经常使用天文单位、光年、秒差距这些单位。

• 天文单位（AU）：即太阳和地球之间的平均距离，约1.5亿公里。
• 光年（ly）：光在宇宙真空中沿直线传播了一儒略年（365.25天）时间的距离，约94607亿千米.
• 秒差距（pc）：以地球公转轨道的平均半径（一个天文单位）为底边所对应的三角形内角称为周年视差。当这个角的大小为1角秒时，这个三角形的一条边的长度（地球到这个恒星的距离）就称为1秒差距。约为3.26光年。

前两个单位我们经常见到，第三个很多不了解的人看了上面的定义也很迷糊，简单的说，1秒差距是周年视差为1”时天体的距离。

0x02 周年视差

而秒差距中所说的周年视差又是什么？在说周年视差的概念之前我们先来看看视差是什么。
视差就是从有一定距离的两个点上观察同一个目标所产生的方向差异。从目标看两个点之间的夹角，叫做这两个点的视差角，两点之间的距离称作基线。只要知道视差角度和基线长度，就可以计算出目标和观测者之间的距离。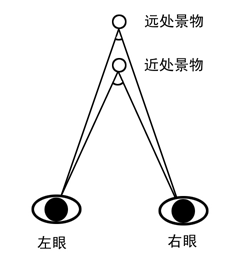

就像当你伸出一个手指放在眼前，先闭上右眼，用左眼看它；再闭上左眼，用右眼看它，会发现手指相对远方的物体的位置有了变化，这就是从不同角度去看同一点的视差。
而周年视差则是地球绕太阳周年运动的直径作为这个“左右眼”的距离，看天体所产生的视差。
即当恒星与太阳的连线垂直地球轨道半径时，恒星对日地平均距离d所张的角ρ叫恒星的周年视差。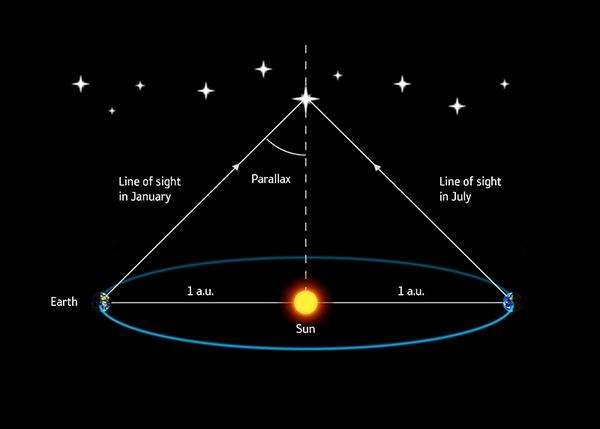

0x03 天体距离的计算

介绍了上面的这些定义，我们来看看天体距离的计算
当ρ为被测天体相对地球轨道半长径的夹角，a为地球公转轨道半长轴，d为天体距离时，距离的计算是：

在这里角度极小情况下sin（ρ）近似为ρ，a为一个天文单位，所以最终距离为周年视差（以秒为单位时）的倒数倍的秒差距。
比如我们的比邻星周年视差为0.76”，则计算距离时：
0.76的倒数为1.32，所以1.32倍的秒差距（3.26光年）为4.3光年。
而建立空间卫星能提升观测距离的真正原因就是因为地面上的望远镜受到大气层影响太大，角分辨率一般不到0.01”，而2013年发射的盖亚空间卫星的角分辨率可以达到0.00001”，大大的增加了观测距离。

0x04 宇宙距离阶梯

虽然通过之前的办法可以观测到很远的地方，但是宇宙的广袤远远超出我们的想像，再远的地方怎么办呢？对于更远的地方，人类就有了其他的观测方案。

在一系列的方法之下，哈勃望远镜眼中的宇宙深处，我们能够观察的宇宙空间直径大约是930亿光年，这个数字是这样得出的：那些从138亿光年外发出的光线，产生这些光线的古老天体，由于宇宙的膨胀，今天它们和我们之间的距离已经达到了大约465亿光年左右。这是我们能观测到的极限半径，乘以二则是我们能够观察的宇宙空间直径，约930亿光年。