0x00 信息加密原理

信息加密是保证数据安全的一种方式。
信息加密的原理是：把明文用加密方法和密钥生成保密的密文，只有使用正确的解密方法和密钥后才能还原出明文。
一个完善的密码体制至少应该满足两个条件：

• 1.已知明文和加密密钥时，容易算出密文和解密过程。
• 2.未知解密密钥时，难以由密文推出明文。

这里介绍以下三种古典密码的加密方式:

• Vernam密码
• Hill密码
• Enigma密码

0x01 Vernam密码

弗纳姆密码相比前面几种古典密码，不同处在于对其对应位的二进制数字进行异或操作，可以简单的表示为：

密文（2进制）=明文（2进制） ⊕ 密钥（2进制）

相反，解密过程就成了：

明文（2进制）=密文（2进制） ⊕ 密钥（2进制）

Vernam密码的核心就是密钥构造的方法，可以使用很长的密钥。虽然长密钥会使得密钥分析变的很困难，但是在大量样本的情况下，使用已知的部分明文序列，对破译帮助很大。

而Vernam密码的改进方案则是号称永不可破译的“一次一密”，因为其密文与明文没有任何的统计关系，使穷举法破译过程永远无法停止，但是这种方法有个额外的困难，那就是密钥要在发送者和接收者之间传递，保存并保护，传递过程很容易出现问题，所以“一次一密”很少被使用。

0x02 Hill密码

希尔密码是一种多字母加密方法，其原理是矩阵的线性变换。
Hill密码算法取m个连续的明文字母，并用m个密文字母代替。这种替代由m个线性方程决定，其中每个字符被分配一个数值（a-z对应0-25）。
如m=3，可以用方程描述如下：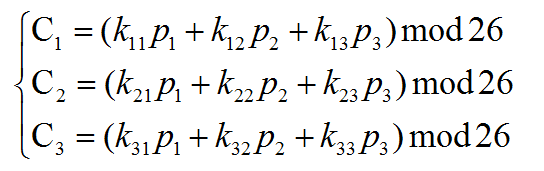

用向量可以表示为：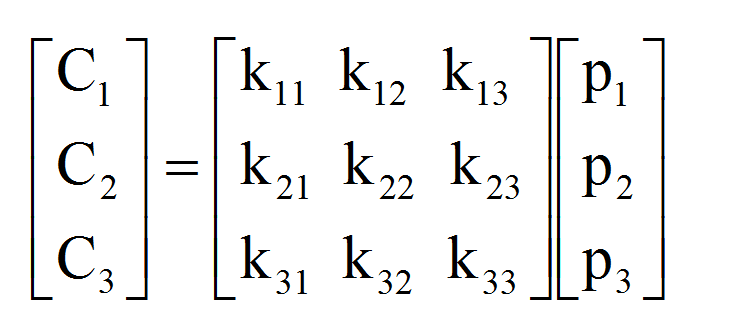

即C=K·P，其中C是密文，P是明文，K是一个密钥矩阵，K·P计算完成后进行模26运算，即可得到密文的对应数值矩阵，然后再转换为密文字母即可。

解密时，只需要求密钥矩阵K的逆矩阵K’，然后P=K·C计算完成后取模26运算，即可得到明文对应数值的矩阵，再转换为明文字母即可。

Hill密码的优点在于能完全隐藏单字母的统计频率，3×3的Hill密码还隐藏了两个字母的频率信息，如果矩阵维度更大，则可以隐藏更多的频率信息。
但是Hill密码的缺点在于，如果同时知道明文和密文，攻破难度就会大大降低。

0x03 Enigma密码

Enigma密码又称为转子机密码，Enigma加密和解密需要一台类似打字机的设备，设定初始位置之后，通过输入明文，设备经过加密输出密文。解密时通过机械装置的切换，实现逆过程解密操作，输入密文，输出明文。
Enigma加密设备由一系列独立转动的圆柱体组成。每个圆柱体有26个输入引脚和26个输出引脚，其内部连线将每个输入引脚连接到一个相应的输出引脚。
如一个圆柱体的机器，每次输入一个明文字母，输出一个对应的密文字母，然后圆柱体旋转一格位置，然后再输入一个同样的明文字母的时候，因为之前的位置已经改变，所以密文字母也会不同，这就定义了一个不同的单字母替代密码。当连续输入26个字母之后，圆柱体又回到了原来的位置，这个时候我们就得到了以26为周期的多字母替代算法。
一个圆柱体看上去很简单，但是当增加圆柱体的数量，我们就可以得到更复杂的多字母替代算法：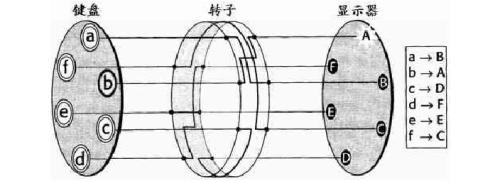

如三个圆柱体分别为快速转子，中速转子和慢速转子：

• 每输入一个明文字母，快速转子动一格
• 快速转子转动够一周，中速转子转动一格
• 中速转子转动够一周，慢速转子转动一格
  
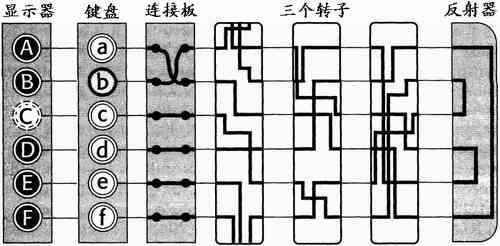
  这样我们就可以得到26×26×26种不同的替代字母，密码强度就会大大提高。