0x00 神经网络

人工神经网络（Artificial Neural Network，缩写ANN），简称神经网络（Neural Network，缩写NN），是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。

0x01 神经元

一个神经元通常具有多个树突，主要用来接受传入信息；而轴突只有一条，轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接，从而传递信号。这个连接的位置在生物学上叫做“突触”。

人脑中神经元如图：

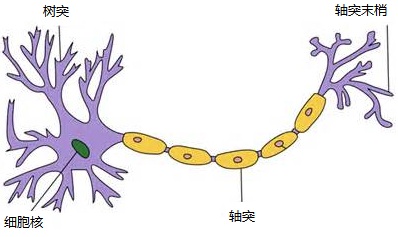
0x02 神经元的数学模型

神经元模型是一个包含输入，输出与计算功能的模型。输入可以类比为神经元的树突，而输出可以类比为神经元的轴突，计算则可以类比为细胞核。

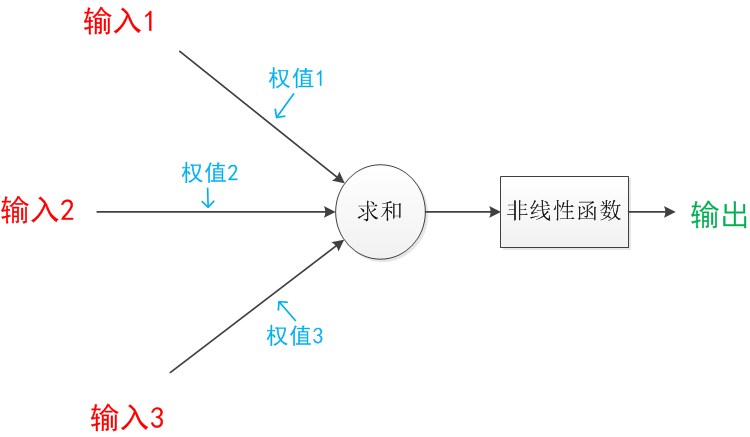
每个连线上都会分配一个权值，在数据传向下一层的时候要乘以对应的权值。在神经网络中，每个箭头表示值的加权传递。

如果我们将神经元图中的所有变量用符号表示，并且写出输出的计算公式，就会得到：

z是在输入和权值的线性加权和叠加了一个激活函数g的值。在MP模型里，函数g是sgn函数，也就是取符号函数。这个函数当输入大于0时，输出1，否则输出-1。

接下来我们将sum函数与sgn函数合并到一个圆圈里，代表神经元的内部计算。其次，把输入a与输出z写到连接线的左上方，便于后面画复杂的网络。一个神经元可以引出多个代表输出的有向箭头，但值都是一样的。

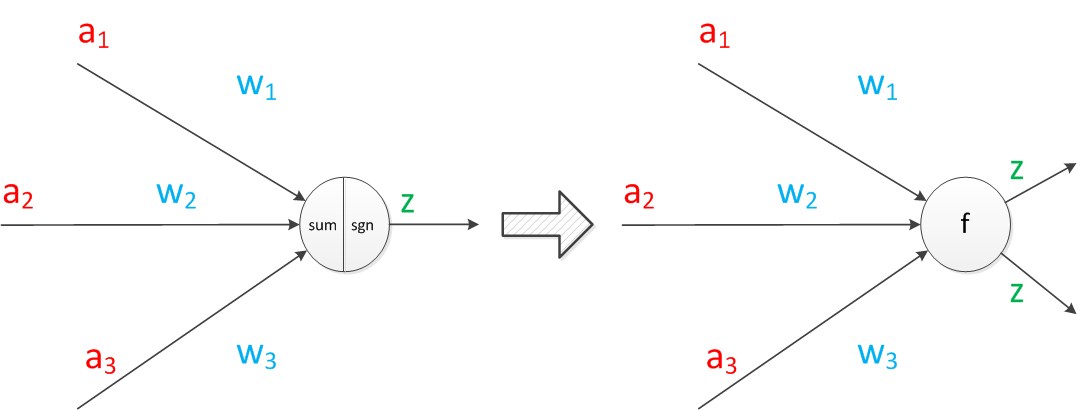
在其他类型神经网络中，这里的激活函数可以有很多种形式：

• 线性函数

• 阈值函数

• Sigmoid函数

• 对称Sigmoid函数

• 双曲正切函数

• 高斯函数

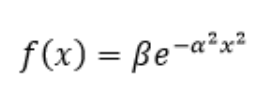
神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果，并传递到下一层。

一个神经网络的训练算法的功能就是通过大量的样本数据训练，让权重的值调整到最佳，以使得整个网络的预测效果最好。然后用来在已知所有输入值的情况下预测输出值。

0x03 单层神经网络(感知器)

感知器(Perceptron)由两层神经元组成的神经网络。两层分别是输入层和输出层，输入层只负责传输数据，输出层对前一层传输过来的数据进行计算。

结构如下：

其中，需要计算的层次也被称为计算层，因为感知器拥有一个计算层，所以称之为“单层神经网络”。

感知器中，我们把 w 称为权重向量，a 称为训练样本。

感知器数据分类的算法步骤如下：

把 w 初始化为 0，或者把 w 的每个分量初始化为[0, 1]之间的任意小数；
把训练样本 a 输入感知器，得到分类结果 z （-1或1）；
根据分类结果更新权重向量。

权重更新算法：

wj=wj+∇wj

∇wj=η∗(z−z′)∗aj

其中

• η 是学习率，在 [0,1] 之间。
• z 是输入样本的正确分类，z’ 是感知器计算出来的分类。

假设初始w=[0,0,0],a=[1,2,3]，z=1，z’=-1时，通过算法计算：

∇w0=0.3∗(1−(−1))∗x0=0.3∗2∗1=0.6

w0=w0+∇w0=0.6

∇w1=0.3∗(1−(−1))∗x1=0.3∗2∗2=1.2

w1=w1+∇w1=1.2

∇w2=0.3∗(1−(−1))∗x2=0.3∗2∗3=1.8

w2=w2+∇w2=1.8

得到更新后的w=[0.6,1.2,1.8]

我们在输入大量样本时，每次在答案正确时不会更改，每次在答案错误时更新权值，只要取的学习率和样本量合适，就可以得到学习之后更为精准的算法。

我们可以看到，感知器类似一个逻辑回归模型，可以做线性分类任务。

我们可以用决策分界来形象的表达分类的效果。决策分界就是在二维的数据平面中划出一条直线，当数据的维度是3维的时候，就是划出一个平面，当数据的维度是n维时，就是划出一个n-1维的超平面。

0x04 两层神经网络(多层感知器)

两层神经网络也就是多了一层计算层(被称为隐藏层)，在增加了这一层之后，神经网络就可以解决一些复杂的问题。

此时，权值矩阵增加到两个，计算层数分为隐藏层计算和输出层计算。

不过不同于单层的sgn函数，在两层神经网络中，我们使用的激活函数最多的是sigmoid函数。

隐藏层计算如图：

输出层计算如图：

总的计算公式：

g(W(1) * a(1)) = a(2);

g(W(2) * a(2)) = z;

与单层神经网络不同。理论证明，两层神经网络可以无限逼近任意连续函数。也就是说，面对复杂的非线性分类任务，两层（带一个隐藏层）神经网络可以分类的很好。

如下例，红色的线与蓝色的线代表数据。而红色区域和蓝色区域代表由神经网络划开的区域，两者的分界线就是决策分界。

0x05 多层神经网络

延续两层神经网络,在两层神经网络的输出层后面，继续添加层次。原来的输出层变成中间层，新加的层次成为新的输出层。我们这样依次添加，就会产生多层神经网络。

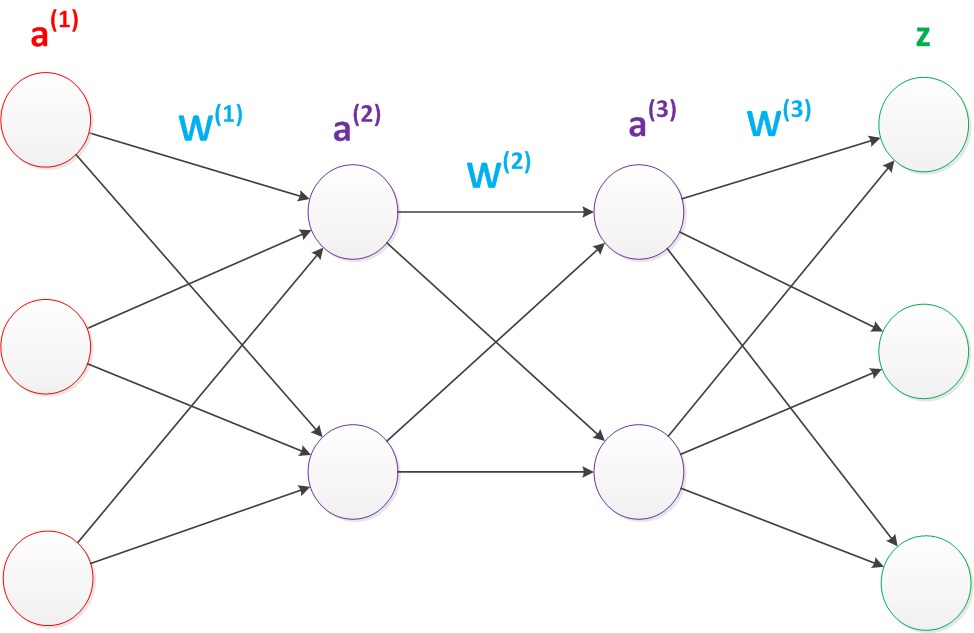
增加了层数，那么正向传播计算公式也会增加一步

g(W(1) * a(1)) = a(2);

g(W(2) * a(2)) = a(3);

g(W(3) * a(3)) = z;

再增加层数的话，与上面同理递推即可：

g(W(1) * a(1)) = a(2);

g(W(2) * a(2)) = a(3);

···

g(w(n-1) * a(n-1)) = a(n);

g(W(n) * a(n)) = z;

随着网络的层数增加，每一层对于前一层次的抽象表示更深入。代表着更深入的表示特征，以及更强的函数模拟能力。在参数数量一样的情况下，更深的网络往往具有比浅层的网络更好的识别效率。

相比于单层神经网络的sgn函数和双层神经网络的sigmoid函数，到了多层神经网络时，通过一系列的研究发现，ReLU函数在训练多层神经网络时，更容易收敛，并且预测性能更好。

ReLU函数不是传统的非线性函数，而是分段线性函数。其表达式非常简单，就是y=max(x,0)。简而言之，在x大于0，输出就是输入，而在x小于0时，输出就保持为0。这种函数的设计启发来自于生物神经元对于激励的线性响应，以及当低于某个阈值后就不再响应的模拟。