0x00 模型评估与选择

在机器学习中，我们需要对使用的模型进行评估，对误差等进行分析，来选择一个预测准确率最高的模型。

0x01 误差

我们把学习器的实际预测输出与样本的真实输出之间的差异称为误差。

• 经验误差：学习器在训练集上的误差称为训练误差或经验误差。

• 泛化误差：将训练好的模型用在新样本上的误差称为泛化误差。

机器学习的目的是为了预测新样本的情况，所以我们需要在新样本上表现很好的学习器，即需要得到一个泛化误差小的学习器。

0x02 过拟合与欠拟合

• 过拟合：学习器把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，导致泛化性能下降。一般是由于学习能力过强，将训练样本所包含的不太一般的性质都学到了。

• 欠拟合：学习器学习能力过弱，对训练样本的一般性质尚未学好

欠拟合比较容易克服，可以在决策树学习中扩展分支、在神经网络中增加训练轮数等。

过拟合则难克服，过拟合是机器学习面临的关键障碍，各类学习算法都有一些针对过拟合的措施来缓解过拟合。

0x03 评估方法

为了对学习器的泛化误差进行评估，需要使用一个测试集来测试学习器对新样本的判别能力，然后以测试集上的测试误差作为泛化误差的近似。

测试集应该尽量与训练集互斥，即测试样本尽量不在训练集中出现、未在训练集中使用过。

下来介绍几种常用的评估方法：

留出法

留出法是直接将数据集D划分为两个互斥的几何，其中一个集合作为训练集S，另一个作为测试集T。

在训练集S中训练出模型后，用测试集T来评估其测试误差，作为对泛化误差的估计。

训练/测试集要尽可能的保证数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响。具体做法是尽可能保留类别比例，最好使用分层采样的方法。

交叉验证法

交叉验证法先将数据集D划分为k个大小相似的互斥子集，每个子集尽可能的保证数据分布的一致性。
然后每次使用k-1个子集作为训练集，余下的一个子集作为测试集。
这样就可以得到k组训练/测试集，可以进行k次训练和测试，最终返回的是k个测试结果的均值。

交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值。
通常将交叉验证法称为“k折交叉验证”。如k取10，则称为10折交叉验证。

留一法

如果数据集D中包含m个样本，若令k=m，则得到了交叉验证法的一个特例：留一法。

显然，留一法不受随机样本划分方式的影响，因为留一法只有唯一一种划分方式。

留一法的评估结果往往被认为比较准确。但是留一法也存在缺陷，当数据集较大时，训练m个模型的计算开销非常大。比如我们是上千万级的数据，那么就得训练上千万个模型，这是不现实的。

自助法

上述几种方法都存在一个问题，那就是由于保留了一部分样本用于测试，导致实际评估的模型所使用的训练集比D小，会引起一些误差，而自助法，可以解决这个问题。

自助法以自助采样法为基础，给定包含m个样本的数据集D，对它进行采样产生数据集D’：
每次随机从D中挑选一个样本，再将样本放回初始数据集中，使得该样本在下次采样时仍有可能被采到。这个过程重复执行m次后，我们就得到了包含m个样本的数据集D’，这就是自助采样的结果。

D中有一部分样本会在D’中多次出现，而另一部分样本不出现。可以做一个简单的估计，样本在m次采样中始终不被采到的概率是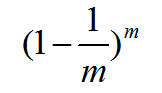

取极限得到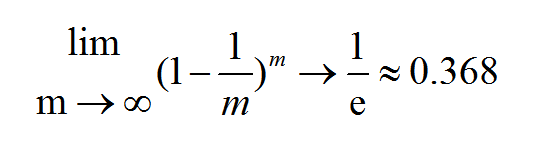

即通过自助采样，初始数据集中约有36.8%的样本未出现在采样数据集D’中，于是我们可以将D’用作训练集，D-D’用作测试集，这样世纪评估的模型与期望评估的模型都使用了m个训练样本，而我们仍然有数据总量36.8%、未在训练集中出现的样本用于测试。这样的测试结果，也被称为“包外估计”。

自助法在数据集较小、难以有效划分训练/测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。

自助法的缺陷是：自助法产生的数据集改变了初始数据集的分布，这会引入估计误差。

所以在初始数据集够用的情况下，留出法和交叉验证法更常用。

0x04 调参与最终模型

大多数学习算法都有参数需要设定，参数配置不同，学得模型的性能往往有显著差别。因此，在进行模型评估与选择时，除了要对适用学习算法进行选择，还需要对算法参数进行设定，这就是通常所说的“参数调节”。

给定包含m个样本的数据集D，在模型评估与选择过程中由于需要留出一部分数据进行评估测试，事实上我们只使用了一部分数据训练模型。因此，在模型选择完成后，学习算法和参数配置已选定，我们要用数据集D重新训练模型，使用所有的m个样本。这时产生的模型才是最终模型。