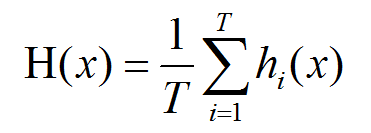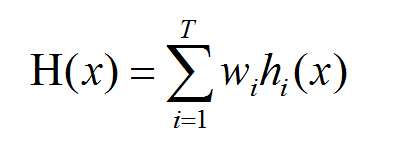0x00 前言

在我们设计的机器学习算法性能达到瓶颈却不满足我们的需求时，我们想在单一的学习器上提升精度需要投入大量的资源，很容易得不偿失。这个时候更好的做法是使用一种优化的策略来提升精度，那就是集成学习。

0x01 集成学习

现实生活中，我们经常会通过投票的方式，以做出更加可靠的决策。集成学习就与此类似。集成学习就是通过构建多个学习器，并通过一定的学习策略将他们结合起来。

集成学习通过将多个学习器进行结合，一般可获得比单一学习器显著优越的泛化性能。

0x02 分类

以个体学习器的类型分类

• 在集成中只包含同种类型的个体学习器，被称为同质集成。如：“决策树集成”，“神经网络集成”。
• 在集成种包含不同种类型的个体学习器，被称为异质集成。如同时包含决策树和神经网络。

以个体学习器的生成方式分类

• 个体学习器之间存在较强的依赖关系，则需要使用串行生成的序列化方法。如：“Boosting”
• 个体学习器不存在强依赖关系，则可使用同时生成的并行化方法。如：“Bagging”、“随机森林”。

0x03 Boosting

Boosting是一种可将弱学习器提升为强学习器的算法，这种算法的工作机制是先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续获得更多关注，然后基于调整后的样本分布来训练下一个基学习器。如此反复，直至基学习器数目达到我们需要的值，最终将这些基学习器进行加权结合。

0x04 Bagging

Bagging是并行式集成学习算法最著名的代表，它基于自助采样法，给定包含m个样本的数据集，我们先随机取出一个样本放入采样器中，再把该样本放回数据集，这样下次该样本仍可能被选中，经过m次随机采样操作，我们得到含有m个样本的采样集，初始训练集中有的样本多次出现，有的样本从未出现。

按照这种方法抽样出T个含m个样本的样本集，然后基于每个样本集训练一个基学习器，再将这些基学习器进行结合，就是Bagging。

0x05 随机森林

随机森林是Bagging的一个扩展变体，随机森林在以决策树为基学习器构建Bagging的基础上，进一步在训练过程中引入随机属性选择。

传统决策树在选择划分属性时是在当前结点的属性集合(共d个)中选择一个最优属性，而随机森林对决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，然后再从这k个属性中选择最优属性进行划分。

很显然，k控制了随机性：

• 如果k和总属性量相同，那就是传统决策树，随机性最低；
• 如果k=1，则随机选择一个属性用于划分，随机性最高。

所以一般情况下，推荐选用k=log2（d）。

0x06 结合策略

之前多次提到了“结合”一词，但是究竟怎么将多个学习器的结果结合起来，也有很多种不同的策略。

下面给出一些常见的策略

平均法

对于回归任务的数值型输出，常见的策略是平均法

简单平均法

简单平均法就是将所有的学习器结果做算数平均，将平均数做为最终结果。

加权平均法

加权平均法是给予每一个学习器不同的权重，加权平均法的权重一般从训练数据中学习得到。

投票法

对于分类任务的标记型输出，常见的策略是投票法

绝对多数投票法（硬投票）

绝对多数投票法即某标记的得票数过半，则预测为该标记，否则拒绝预测。

相对多数投票法（硬投票）

相对多数投票法即预测为得票最多的标记，若同时有多个最高票，则从中随机选取一个。

加权投票法（软投票）

加权投票法会返回预测各个类的概率加权平均值，然后取其中最大平均概率的分类做为预测结果。

可以用表格清晰的表示出来

分类器	类别1	类别2	类别3
分类器1	w1*0.2	w1*0.5	w1*0.3
分类器2	w2*0.6	w2*0.3	w2*0.1
分类器3	w3*0.3	w2*0.4	w2*0.3

在预测时，计算每一类的加权平均值比较即可。